Как привести дроби к наименьшему общему знаменателю

Чтобы привести несколько дробей к наименьшему общему знаменателю, надо:

1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;

2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;

3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Пример: приведем к наименьшему общему знаменателю дроби 3/4 и 5/6.

1) Находим наименьшее общее кратное (НОК) чисел 4 и 6. Это 12. То есть 12 – минимальное число, на которое делятся без остатка и 4, и 6.

2) Делим 12 на знаменатель каждой из двух дробей, чтобы найти их дополнительные множители:

12 : 4 = 3, 12 : 6 = 2.

Таким образом, дополнительным множителем дроби 3/4 является 3, дроби 5/6 – 2.

3) Чтобы в знаменателе обеих дробей было число 12, надо умножить их числители и знаменатели на их дополнительные множители.

Нашли общий знаменатель двух дробей – число 12.

В дроби 3/4 делим 12 на знаменатель 4 и полученный результат умножаем на числитель 3:

Мы получили числитель. Итак, в числителе у нас 9, в знаменателе 12:

В дроби 5/6 делим 12 на 6 и полученный результат умножаем на 5:

Как привести дроби к наименьшему общему знаменателю

Наименьшим общим знаменателем (НОЗ) данных несократимых дробей является наименьшее общее кратное (НОК) знаменателей этих дробей. (см. тему «Нахождение наименьшего общего кратного»: 5.3.5. Нахождение наименьшего общего кратного (НОК) данных чисел ).

Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Примеры. Привести следующие дроби к наименьшему общему знаменателю.

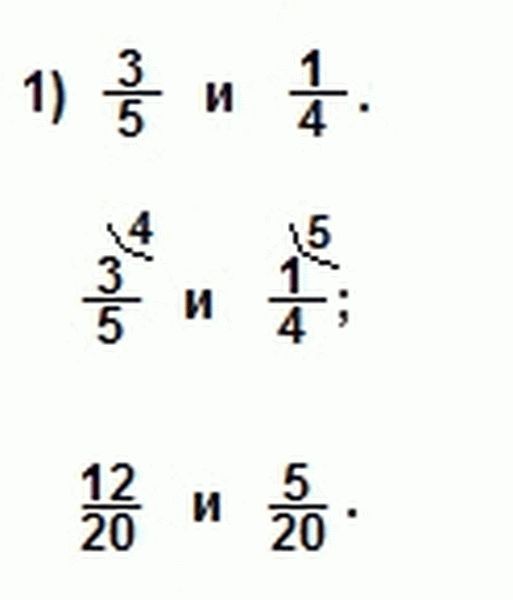
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20:5=4). Для 2-й дроби дополнительный множитель равен 5 (20:4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20).

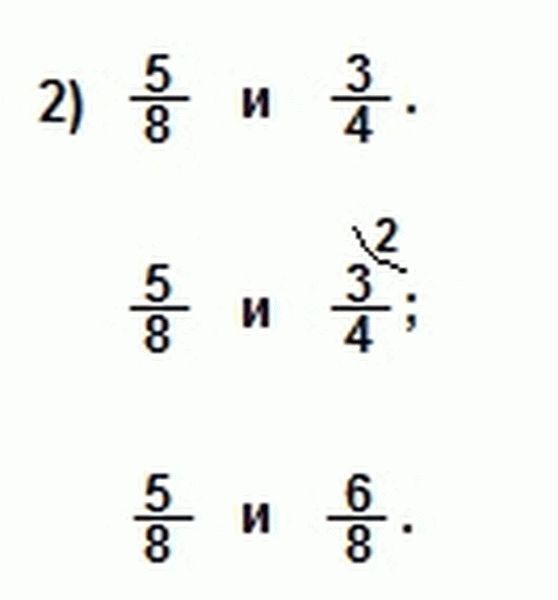
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8:4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8).

Данные дроби не являются несократимыми.

Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей ). Находим НОК(16; 20)=2 4 ·5=16·5=80. Дополнительный множитель для 1-й дроби равен 5 (80:16=5). Дополнительный множитель для 2-й дроби равен 4 (80:20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80).

Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30:5=6), дополнительный множитель ко 2-й дроби равен 5 (30:6=5), дополнительный множитель к 3-ей дроби равен 2 (30:15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30).

Приведение дробей к наименьшему общему знаменателю

Дроби могут иметь множество общих знаменателей.

Могут иметь общие знаменатели: 4, 8, 12, 16 и т.д.:

В множестве чисел, являющихся общим знаменателем данных дробей существует наименьшее натуральное число, которое называют наименьшим общим знаменателем.

Таким образом, из всех общих знаменателей 4, 8, 12, 16 дробей:

наименьшим общим знаменателем будет знаменатель 4, так как число 4 – наименьшее натуральное число из чисел 4, 8, 12, 16.

Определение наименьшего общего знаменателя

Наименьший общий знаменатель – это наименьшее число из всех общих знаменателей данных дробей.

Наименьший общий знаменатель будет равен 36.

Чтобы найти наименьший общий знаменатель дробей, нужно найти наименьшее общее кратное (НОК) этих знаменателей.

Как привести дроби к наименьшему общему знаменателю

Шаг 1

Найти наименьший общий знаменатель.

Шаг 2

Найти дополнительный множитель.

Шаг 3

Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Шаг 4

Записать полученные дроби с новым знаменателем.

Пример 1

Привести дроби к общему знаменателю и наименьшему общему знаменателю::

Действие 1

Найдем общий знаменатель для рассматриваемых дробей.

Чтобы найти общий знаменатель, перемножим знаменатели:

Дополнительный множитель к первой дроби:

Дробь примет вид:

Дополнительный множитель ко второй дроби:

Дробь примет вид:

Дополнительный множитель к третьей дроби:

Дробь примет вид:

Итак, были дроби:

Запишем полученные дроби с общим знаменателем:

Действие 2

Приведем дроби к наименьшему общему знаменателю:

Чтобы привести дроби к наименьшему общему знаменателю нужно:

1. Найти наименьший общий знаменатель. Чтобы найти наименьший общий знаменатель, нужно найти наименьшее общее кратное (НОК) этих дробей. Оно и будет наименьшим общим знаменателем.
2. Найти дополнительный множитель. Для этого наименьший общий знаменатель разделим на знаменатели данных дробей.
3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
4. Записать полученные дроби с новым знаменателем.

Шаг 1

Чтобы найти наименьшее общее кратное (НОК) нужно знаменатели дробей разложить на множители.

Разложим их знаменатели на множители:

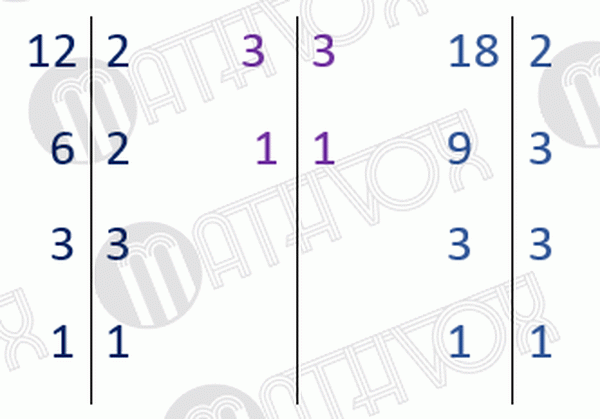
Запишем знаменатели как произведение множителей:

Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:

Наименьший общий знаменатель у этих дробей: 36.

Шаг 2

Находим дополнительные множители для этих дробей. Для этого 36 делим на 12, 3, 18 (знаменатели этих дробей):

Шаг 3

Умножим числители и знаменатели этих дробей на дополнительные множители:

Таким образом эти дроби привели к наименьшему общему знаменателю.

Ответ

приведенные к общему знаменателю:

приведенные к наименьшему общему знаменателю:

Пример 2

Привести к наименьшему общему знаменателю дроби:

Решение

Шаг 1

Найдем наименьший общий знаменатель. Для этого определим НОК. Чтобы найти НОК, разложим знаменатели на простые множители.

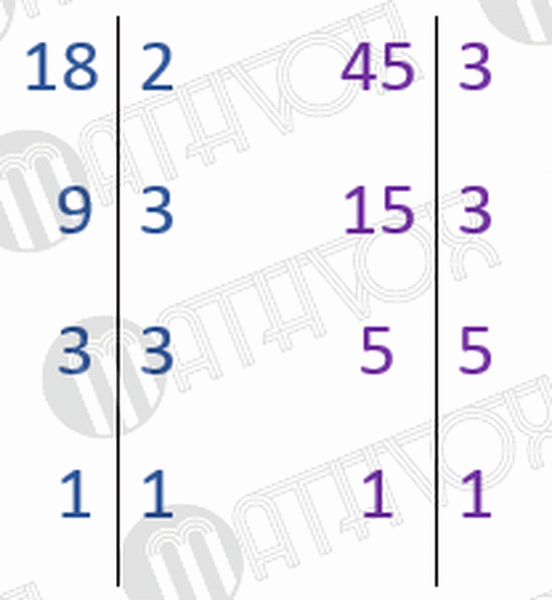
Представим знаменатели в виде произведения множителей:

Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:

Наименьший общий знаменатель 90.

Шаг 2

Найдем дополнительные множители для этих дробей. Для этого 90 делим на 18, 45 (знаменатели этих дробей):

Шаг 3

Умножим числители и знаменатели этих дробей на дополнительные множители:

Таким образом эти дроби привели к наименьшему общему знаменателю.

Ответ

приведенные к наименьшему общему знаменателю имеют вид:

Как привести дробь к НОЗ

Чтобы можно было выполнять операции сложения, вычитания и сравнения между простыми дробями, у них должны быть одинаковые знаменатели.

Если знаменатели дробей различны (именно так чаще и бывает), дроби следует привести к общему знаменателю.

Общим знаменателем называют число, кратное каждому из первоначальных знаменателей исходных дробей.

Наименьшим общим знаменателем (НОЗ) называют наименьший из всех возможных знаменателей или наименьшее общее кратное знаменателей исходных дробей.

Правило приведения двух дробей к НОЗ:

• находим наименьшее общее кратное(НОК) знаменателей;
• для каждой дроби назодим дополнительный множитель — число, на которое следует умножить знаменатель дроби, чтобы получить НОК знаменателей (для этого следует разделить НОК на знаменатель каждой из дробей);
• умножаем числитель и знаменатель каждой дроби на ее дополнительный делитель.

ПРИМЕР: Найти НОЗ дробей 18/81 и 13/45.

Дополнительный множитель для дроби 18/81 будет равен 5; для дроби 13/45 равен 9.

Умножаем числитель и знаменатель первой дроби на 5, а второй — на 9, после чего получаем две дроби с одинаковыми знаменателями: 90/405 и 117/405.

Задача 1: Что больше 14/19 или 27/33.

• НОК(19;33) = 627
• 627/19 = 33
• 627/33 = 19
• 14 · 33 = 462
• 27 · 19 = 513
• 14/19 = 462/627
• 27/33 = 513/627
• 462 Если вам понравился сайт, будем благодарны за его популяризацию :) Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:

»

Дата публикации: 29.05.2019