Привести уравнение прямой к каноническому виду
Общие уравнения прямой
(*)
преобразовать к каноническому виду (1).
Из системы (*) исключим сначала y и выразим z через x, потом исключим x и выразим z уже через y.
1) Для того, чтобы из системы (*) исключить y, умножим второе из уравнений системы (*) на 3 и сложим его почленно с первым. Получим, что 7x — z — 7 = 0, откуда z = 7x — 7,
2) Умножая первое уравнение из (*) на -2 и складывая почленно со вторым, получим, исключая x из системы (*),
Привести уравнение прямой к каноническому виду
Привести уравнение прямой к каноническому виду
Уравнение прямой: 9x^2+4xy+6y^2+2x-4y-4=0; Ребят, никак не могу разобраться в данном вопросе.
Привести уравнение прямой к каноническому виду
(x-2)^2=25*((x-4)^2+(y+3)^2) Хотелось бы увидеть пошаговое решение. Заранее спасибо.
Привести к каноническому виду общие уравнения прямой
Привести к каноническому виду общие уравнения прямой begin 2x-4y+3z+4=0 & text < >\ .
Определить вил прямой и привести к каноническому виду
Определить вил прямой и привести к каноническому виду x^2-x+8=y
привести уравнение к каноническому виду
привести уравнение к каноническому виду z=x^2+y^2-4x+2y и определить тип поверхности
Решение задач
Привести к каноническому виду общие уравнения прямой l.
Задача представлена репетитором по высшей математике Быстровым Александром Анатольевичем.
Прямая задана общими уравнениями, которые представляют систему двух уравнений
По условию задачи имеем коэффициенты равными
Решение:
По существу данная система уравнений представляет два уравнения для плоскостей Р1 и Р2. Данные плоскости имеют соответственные нормальные векторы N1 и N2 , то есть перпендикулярные к этим плоскостям. Причем координаты векторов определяются коэффициентами уравнений N 1 (A1,B1,C1) N 2 (A2,B2,C2).
Необходимо составить уравнения в каноническом виде
1) Находим координаты точки М( x 0, y 0, z 0), которая лежит на прямой l. Положим z 0=0 и запишем систему исходных уравнений для прямой l , положив в них z =0:
Решим эту систему уравнений и получим x0=-1, y0=1 .
То есть мы нашли координаты точки М ( x 0 =-1, y 0 =1, z 0=0).
2) Нам необходимо определить координаты направляющего вектора N(l,m,n). Тогда уравнение прямой в каноническом виде имеет вид:
3)Составляем направляющий вектор N(l,m,n) . Он находится, как векторное произведение нормальных векторов плоскостей, которые при пересечении образуют линию l, из исходной системы уравнений
Записываем векторное произведение, как определитель по тройке векторов i, j, k:
| i | j | k |
| A1 | B1 | C1 |
| A2 | B2 | C2 |
=li+mj+nk
Подставляем наши значения:
| i | j | k |
| 2 | 0 | -3 |
| 0 | 1 | 5 |
=(0·5-(-3)·1)i-0·(2·5-0·(-3))j+(-3)·(2·1-0·0)k=3·i+0·j+(-6)·k
То есть нашли вектор N(l=3,m=0,n=-6).
4) Записываем уравнение нашей прямой l в каноническом виде:
.Итак, мы привели к каноническому виду общие уравнения прямой.
Популярные репетиторы:

Когда еще учился в аспирантуре, я мечтал собрать вместе 2 моих основных пристрастий: Математику и Обучение, c самого истока своей карьеры.
Безупречный математик для школьников и студентов, кандидат физмат. наук, докторант, педагогический стаж более 15 лет, самолетом подготовит без посредников учащихся к экзамену в институте по математике в 10 класс с помощью тайных способов по усовершенствованию памяти и мед-допинг мышления.
Впечатляюще поработал по развитию в стартапе по Нейронным сетям и Машинному обучению. Шутя программирует на JavaScript, Perl и Scala. Участвует в ведущих научных симпозиумах ACL, ICCV и WWW . Консультации по математическим программам Microsoft Mathematics, MathLab и Maple .
Занятия ведутся в Москве м. Китай-город и дистанционно по Viber. Опыт учителя по высшей математике для аспирантов более 20 лет. Более 320 учащихся поступили «на бюджет» в ВУЗы Москвы: МГУ, МЭИ, Школа Анализа Данных Яндекса и ВШЭ и многие другие. Er spricht Deutsch.
Каноническое уравнение прямой на плоскости
В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.
Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.
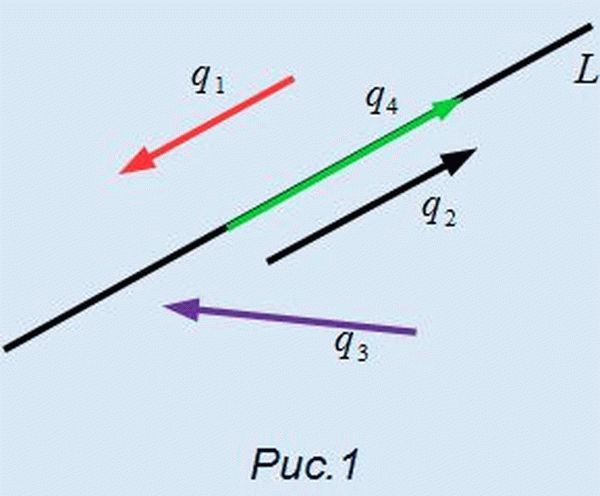 |
На рисунке Рис.1 представлена прямая L и векторы q1, q2, q3, q4. Из определения следует, что векторы q1, q2, q4 являются направляющими векторами прямой L, а q3 − нет.
Каноническое уравнение прямой L на плоскости представляется следующей формулой:
| (1) |
где x1, y1 координаты некоторой точки M1 на прямой L. Вектор q=<m, p> является направляющим вектором прямой L.
Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к. направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя. В этом можно убедится, записав уравнение (1) в следующем виде:
| . | (2) |
Выше мы отметили, что прямая L проходит через точку M1(x1, y1). В этом можно убедится, подставив x=x1, y=y1 в уравнение (1).
| . | (3) |
Чтобы убедится, что точки M1(x1, y1) и M2(x2, y2) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M1 и M2. Получим тождества, следовательно эти точки принадлежат прямой L.
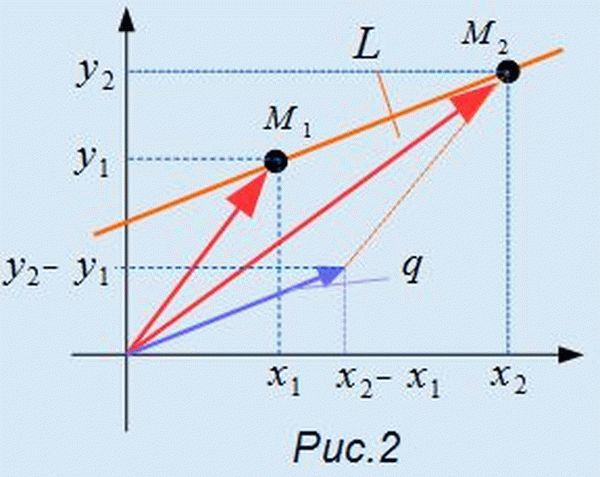 |
Сравним уравнения (1) и (3). Тогда можно записать q=<m, p>=<x2−x1, y2−y1>. На рисунке Рис.2 представлен вектор q, которая является разностью векторов, соответствующих точкам M2 и M1. Этот вектор является направляющим вектором прямой L. Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.
Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.
Онлайн калькулятор, для построения прямой через две точки находится тут.
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
| . |
| . |
Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q=<0, 3>. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
| . |
| . |
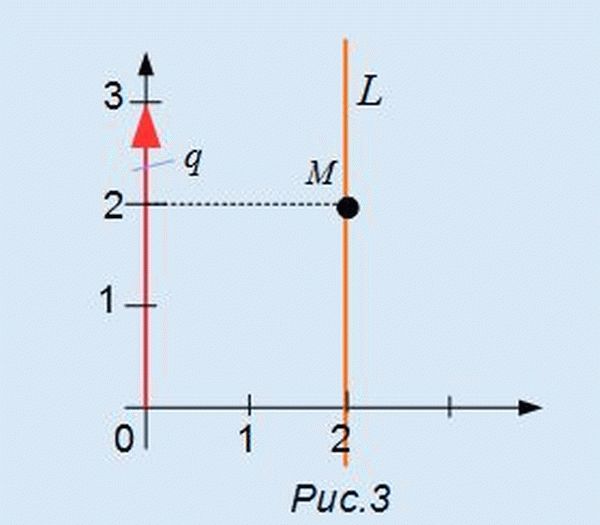
На рисунке Рис.3 изображена прямая L, точка M=(2, 2) и направляющий вектор q=<0, 3>. Прямая проходит через точку M и параллельна направляющему вектору q.
 |
Пример 3. Прямая проходит через точки M1=(−7, 2) и M2=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):
| . |
Упростим полученное уравнение:
| . |
| . |
Приведение канонического уравнения прямой на плоскости к параметрическому виду
Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:
| . |
Выразим переменные x и y через t:
| , | (4) |
где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.
Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.
Обратное преобразование смотрите здесь.
Пример 4. Каноническое уравнение прямой задана следующим уравнением:
| . | (5) |
Найти параметрическое уравнение прямой.
Решение. Обозначим через t левую и правую части уравнения (5):
| . |
Выразим переменные x и y через t:
| . |
| . |
Приведение канонического уравнения прямой на плоскости к общему виду
Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:
| , |
| . | (6) |
Сделаем следующие обозначения:
| A=p, B=−m, C=−px1+my1. |
Тогда уравнение (6) можно записать в следующем виде:
| Ax+By+C=0, |
где n=<A,B> − называется нормальным вектором прямой.
Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:
| (n,q)=(<A,B>,<m,p>) =(<p,−m>,<m,p>)=pm−mp=0. |
Обратное преобразование смотрите здесь.
Пример 5. Каноническое уравнение прямой задана следующим уравнением:
| . | (7) |
Записать общее уравнение прямой.
Решение. Сделаем преобразования уравнения (7):
»
Дата публикации: 29.05.2019